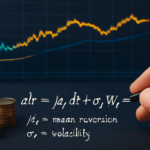Volatility — the measure of how much an asset’s price fluctuates — is a key factor in option pricing and financial risk analysis. Traditional models like the Black-Scholes assume constant volatility, but real markets show that volatility changes over time, often unpredictably. This led to the development of stochastic volatility models, which treat volatility itself as a random process.
Stochastic volatility models offer a more realistic framework for pricing options, managing risk, and understanding market behavior. This article explores the mathematical foundations of these models, their applications in option pricing, and their critical role in risk analysis.

Table of Contents
-
Understanding Volatility in Financial Markets
-
Limitations of Constant Volatility Models
-
What Are Stochastic Volatility Models?
-
The Heston Model: A Popular Stochastic Volatility Model
-
Mathematical Formulation of Stochastic Volatility Models
-
Calibration of Stochastic Volatility Models to Market Data
-
Impact on Option Pricing Accuracy
-
Volatility Smile and Skew Explained
-
Stochastic Volatility and Risk Metrics
-
Monte Carlo Simulations with Stochastic Volatility
-
Extensions: Jump Diffusion and Other Hybrid Models
-
Practical Challenges and Computational Issues
-
Applications Beyond Option Pricing
-
Future Directions in Stochastic Volatility Modeling
-
Conclusion
Understanding Volatility in Financial Markets
Volatility represents the uncertainty or risk associated with the size of changes in an asset’s price. It is often estimated using historical price data or implied from option prices.
Limitations of Constant Volatility Models
The Black-Scholes model assumes volatility is constant, but market data shows volatility:
-
Varies over time (volatility clustering)
-
Exhibits asymmetry (leverage effect)
-
Produces volatility smiles and skews in option prices
Constant volatility models fail to capture these phenomena, leading to mispriced options.
What Are Stochastic Volatility Models?
Stochastic volatility models introduce a second stochastic process to represent the evolution of volatility, usually correlated with the asset price.
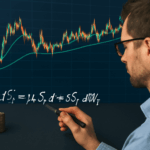
Mathematically, if StS_t is the asset price and vtv_t the variance (volatility squared), models have dynamics like:
{dSt=μStdt+vtStdWt(1)dvt=κ(θ−vt)dt+σvvtdWt(2)\begin{cases} dS_t = \mu S_t dt + \sqrt{v_t} S_t dW_t^{(1)} \\ dv_t = \kappa(\theta – v_t) dt + \sigma_v \sqrt{v_t} dW_t^{(2)} \end{cases}
where dWt(1)dW_t^{(1)} and dWt(2)dW_t^{(2)} are correlated Brownian motions.
The Heston Model: A Popular Stochastic Volatility Model
The Heston model is widely used due to its semi-analytical tractability.
Parameters:
-
κ\kappa: rate of mean reversion
-
θ\theta: long-term variance mean
-
σv\sigma_v: volatility of variance (vol of vol)
-
ρ\rho: correlation between asset and volatility shocks
Mathematical Formulation of Stochastic Volatility Models
Stochastic volatility models are governed by coupled stochastic differential equations (SDEs). Solutions often require numerical methods like Monte Carlo simulation or Fourier transform techniques.
Calibration of Stochastic Volatility Models to Market Data
Calibration involves fitting model parameters to observed option prices, minimizing pricing errors and capturing market-implied volatility surfaces.
Impact on Option Pricing Accuracy
Stochastic volatility models improve:
-
Pricing of out-of-the-money and in-the-money options
-
Capturing volatility smiles/skews
-
Better hedging strategies
Volatility Smile and Skew Explained
These patterns occur because implied volatility varies with strike price and maturity. Stochastic volatility models naturally generate these shapes due to the volatility’s random evolution.
Stochastic Volatility and Risk Metrics
They allow for more accurate estimation of:
-
Greeks (sensitivities)
-
Value at Risk (VaR)
-
Expected Shortfall (ES)

Monte Carlo Simulations with Stochastic Volatility
Monte Carlo methods simulate numerous price and volatility paths to price complex derivatives and estimate risk.
Extensions: Jump Diffusion and Other Hybrid Models
Combining stochastic volatility with jumps in price or volatility better models sudden market moves.
Practical Challenges and Computational Issues
-
Model complexity increases computational load.
-
Calibration may be unstable.
-
Requires high-quality data.
Applications Beyond Option Pricing
Used in:
-
Risk management
-
Portfolio optimization
-
Interest rate modeling
Future Directions in Stochastic Volatility Modeling
-
Machine learning-enhanced calibration
-
Rough volatility models capturing fractional dynamics
-
Real-time risk monitoring tools
Stochastic volatility models provide a powerful framework to understand and price financial derivatives realistically. By modeling the randomness in volatility itself, they offer better accuracy and risk assessment, crucial for traders and risk managers navigating complex markets.