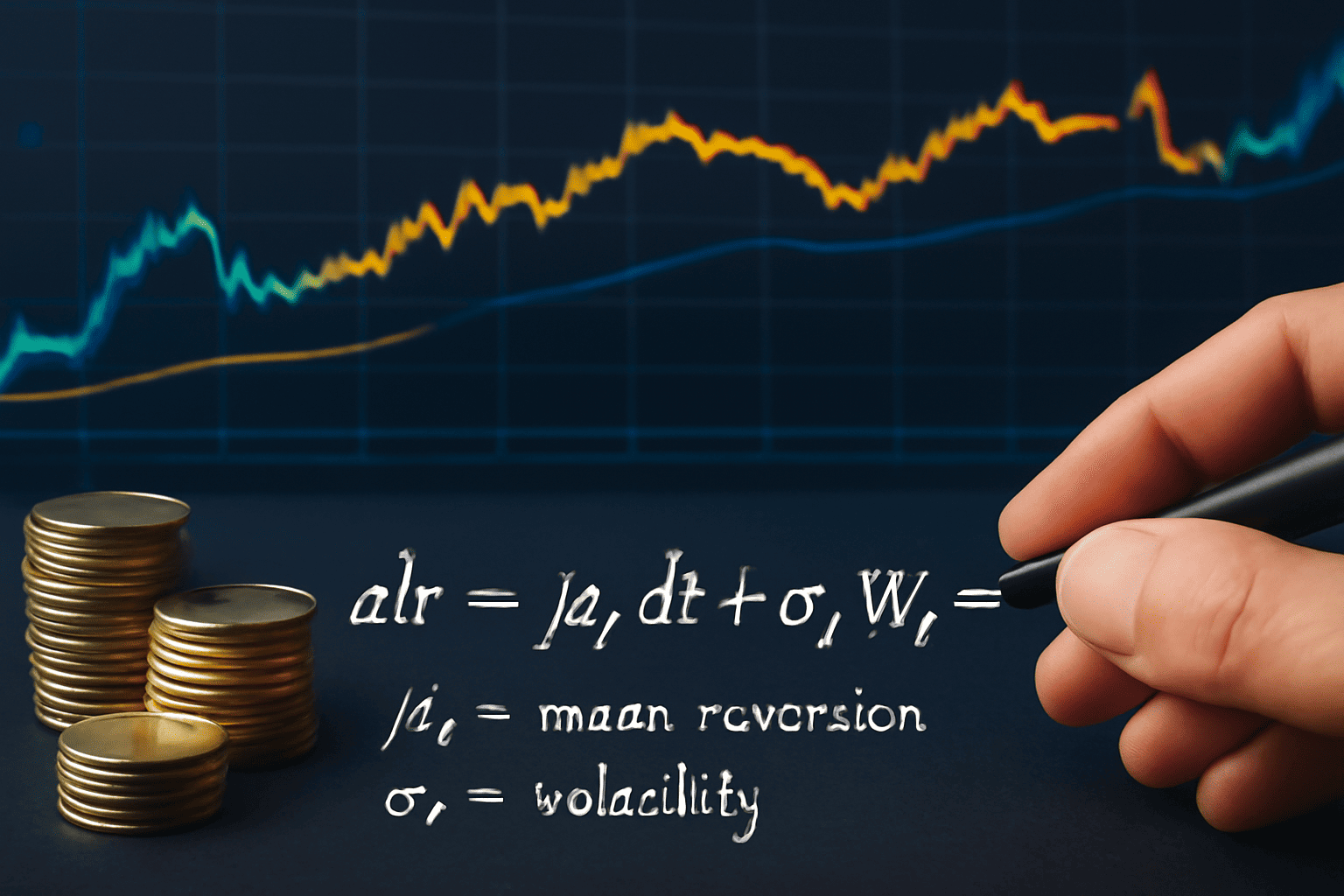The Mathematics of Stochastic Interest Rate Models in Finance

Interest rates are fundamental to the pricing of numerous financial instruments, from bonds and loans to derivatives and mortgage-backed securities. However, interest rates are not static — they fluctuate over time in response to economic conditions, monetary policy, and market dynamics.

To accurately model and predict interest rate movements, financial mathematicians employ stochastic interest rate models. These models use stochastic calculus to capture the random behavior of interest rates, enabling better pricing, hedging, and risk management.

This article explores the mathematical foundations of stochastic interest rate models, their applications, and their importance in modern finance.

Table of Contents

1. Understanding Interest Rate Dynamics

2. Deterministic vs. Stochastic Interest Rate Models

3. Basics of Stochastic Processes

4. The Short Rate and Its Role in Interest Rate Modeling

5. Classical Stochastic Interest Rate Models

   • Vasicek Model

   • Cox-Ingersoll-Ross (CIR) Model

   • Hull-White Model

6. Mathematical Formulation of Key Models

7. Bond Pricing Using Stochastic Interest Rate Models

8. Calibration of Interest Rate Models to Market Data

9. Extensions: Multi-Factor and Affine Models

10. Numerical Methods for Interest Rate Models

11. Applications in Derivatives Pricing and Risk Management

12. Challenges and Limitations

13. Advances in Interest Rate Modeling

14. Conclusion

Understanding Interest Rate Dynamics

Interest rates represent the cost of borrowing money or the return on investment for lending money. They fluctuate based on inflation expectations, central bank policies, credit risk, and macroeconomic factors.

Capturing these dynamics requires models that reflect both deterministic trends and random fluctuations.

Deterministic vs. Stochastic Interest Rate Models

• Deterministic models assume known, fixed interest rate paths.

• Stochastic models incorporate randomness, better reflecting market realities and uncertainty.

Basics of Stochastic Processes

Stochastic models use random processes such as:

• Brownian motion

• Mean-reverting processes

• Jump processes

to model interest rate evolution.

The Short Rate and Its Role in Interest Rate Modeling

The short rate rtr_trt​ is the instantaneous interest rate at time $t$. It serves as the primary variable in many interest rate models, capturing the cost of borrowing over an infinitesimally small time period.

Classical Stochastic Interest Rate Models

Vasicek Model

Defined by the SDE:

drt=a(b−rt)dt+σdWtdr_t = a(b – r_t) dt + \sigma dW_tdrt​=a(b−rt​)dt+σdWt​

• $a$: speed of mean reversion

• $b$: long-term mean rate

• $\sigma$: volatility

• WtW_tWt​: Brownian motion

The model allows negative interest rates due to normal distribution of rtr_trt​.

Cox-Ingersoll-Ross (CIR) Model

Defined by:

drt=a(b−rt)dt+σrtdWtdr_t = a(b – r_t) dt + \sigma \sqrt{r_t} dW_tdrt​=a(b−rt​)dt+σrt​​dWt​

Ensures non-negative interest rates and models volatility proportional to the square root of the rate.

Hull-White Model

An extension of Vasicek with time-dependent parameters:

drt=[θ(t)−art]dt+σdWtdr_t = [\theta(t) – a r_t] dt + \sigma dW_tdrt​=[θ(t)−art​]dt+σdWt​

Allows better calibration to market data.

Mathematical Formulation of Key Models

Models are expressed as stochastic differential equations (SDEs) solved using Itô calculus. Closed-form solutions exist for bond prices under Vasicek and CIR models.

Bond Pricing Using Stochastic Interest Rate Models

The price of a zero-coupon bond is given by:

P(t,T)=Et[e−∫tTrsds]P(t,T) = \mathbb{E}_t \left[ e^{-\int_t^T r_s ds} \right]P(t,T)=Et​[e−∫tT​rs​ds]

Stochastic models enable the calculation of the expected discounted payoff considering the random evolution of rtr_trt​.

 Calibration of Interest Rate Models to Market Data

Parameters $a,b,\sigma$ are estimated by fitting model outputs to:

• Yield curves

• Cap and swaption prices

• Historical interest rate data

Extensions: Multi-Factor and Affine Models

Multi-factor models include several stochastic variables capturing different aspects of the interest rate curve.

Affine models generalize Vasicek and CIR, offering greater flexibility.

Numerical Methods for Interest Rate Models

When closed-form solutions are unavailable, numerical techniques such as:

• Monte Carlo simulation

• Finite difference methods

• Tree methods

are employed.

Applications in Derivatives Pricing and Risk Management

Stochastic interest rate models are crucial for:

• Pricing interest rate derivatives (swaps, caps, floors)

• Managing interest rate risk

• Scenario analysis and stress testing

Challenges and Limitations

• Model risk due to incorrect assumptions

• Calibration complexity

• Computational intensity for high-dimensional models

Advances in Interest Rate Modeling

Recent innovations include:

• Rough volatility models capturing more complex market behaviors

• Machine learning for model calibration

• Integration with macroeconomic models

Stochastic interest rate models provide a mathematically rigorous framework to understand and predict the evolution of interest rates. Their ability to incorporate randomness and mean reversion makes them essential for pricing, hedging, and managing financial risks in fixed income markets.